Collisions in Two Dimensions

An alpha particle collides elastically with a stationary nucleus and continues moving at an angle of $60°$ with respect to the original direction of motion.The nucleus recoils at an angle of $30°$ with respect to this direction. Mass number of this nucleus is

A particle of mass $m$ strikes another particle of same mass at rest elastically. After collision if velocity of one of the particle is $3\hat{i}-2\hat{j} \mathrm{m} {\mathrm{s}}^{-1}$, then the other must have a velocity equals to

For an oblique collision, System momentum is not conserved along the line of impact.

A ball is thrown with velocity u at an angle θ with vertical towards a smooth surface. Find the velocity of ball after collision if coefficient of restitution is e.

Which of the given quantity is vector?

Momentum is scalar quantity.

A ball moving with a certain velocity hits another identical ball at rest. If the plane is frictionless and collision is an elastic oblique collision, the angle between the directions in which the balls move after the collision will be

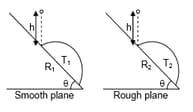
Two balls are dropped from the same height $h$ on a smooth plane and the other on a rough plane having the same inclination $\theta$ with horizontal. Both the planes have the same coefficient of restitution. If the range and time of flight of the first and second balls are $R_1,T_1$ and $R_2,T_2$ respectively. Then what will be the relation between given parameters?

Cotyledons are also called-

A particle $\mathrm{A}$ suffers an oblique elastic collision with a particle $\mathrm{B}$ which is initially at rest. If their masses are same, then after the collision

The coefficient of restitution between a snooker ball and the side cushion is $\frac{1}{3}$. If the ball hits the cushion and then rebounds at right angles to its original direction, then what is the angle made with the side cushion by the direction of motion before and after impact?

4 identical balls of radius R and mass m are lying in a gravity free space. The balls are in contact and their centres are forming vertices of a square of side 2R in horizontal plane. One identical ball travelling vertivally with a speed v hits the four balls symmetrically. The collision is perfectly elastic. The centre of the 4 stationary ball are at $\left(R, R, 0\right), \left(-R, R, 0\right), \left(R, -R, 0\right)$ and $\left(-R, -R, 0\right)$ initially.



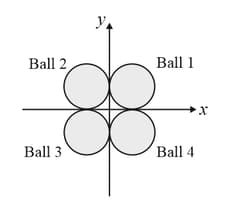
The speed of the ball 1 after collision is:

A ball moving with a certain velocity hits another identical ball at rest. If the plane is frictionless and collision is elastic, the angle between the directions in which the balls move after collision, will be

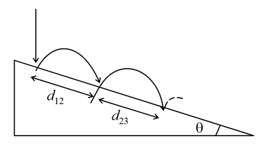
An elastic ball is dropped on a long inclined plane. If bounces, hits the plane again, bounces and so on. let us Label the distance between the point of the first and second hit ${\mathrm{d}}_{12}$ and the distance between the points of second and the third hit is ${\mathrm{d}}_{23}$ . find the ratio of ${{\mathrm{d}}_{12}/\mathrm{d}}_{23}$ .

A ball moving with a certain velocity hits another identical ball at rest. If the plane is frictionless and collision is an elastic oblique collision, the angle between the directions in which the balls move after the collision, will be

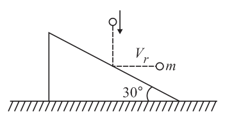
As shown in the figure a body of mass $m$ moving vertically with speed $3 \mathrm{m} {\mathrm{s}}^{-1}$ hits a smooth fixed inclined plane and rebounds with a velocity $v_f$ in the horizontal direction. If $$$\angle$$$ of inclined is $30°$, the velocity $v_f$ will be

A ball strikes a smooth horizontal ground at an angle of $45°$ with the vertical. What cannot be the possible angle of its velocity with the vertical after the collision?.

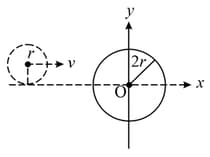
A small smooth disc of mass $\mathrm{m}$ and radius $\mathrm{r}$ moving with an initial velocity $\mathrm{v}$ along the positive $\mathrm{x}$-axis collided with a big disc of mass $2\mathrm{m}$ and radius $2\mathrm{r}$ which was initially at rest with its centre at origin as shown in the figure. If the coefficient of restitution is $0$, then the velocity of the larger disc after the collision is

A ball (initially at rest) falls vertically for $2 \mathrm{s}$ and hits a smooth plane inclined at $30°$ to the horizontal. The coefficient of restitution is $\frac{5}{8}$. The distance along the plane between the first and second impact of the ball is